이번 시간에는 이진트리에 대해 알아보는 시간을 가져보고자 한다. 자세한 메서드 구현 내용보다는 앞으로 정리해 나갈 이진트리에 대한 개요라고 볼 수 있다.
이진 트리
이진트리는 각 노드가 왼쪽 자식과 오른쪽 자식으로 불리는 리프 노드를 갖는 데이터 구조를 의미한다. 이진트리에서 각 노드는 값을 가질 수 있고, 이들은 다시 자신만의 자식 노드를 최대 2개 가질 수 있는 형식으로 아랫 방향으로 뿌리를 넓혀 가는 특징을 보인다.
이진트리 만들기
이진트리의 Node 구조도 앞서 언급한 특성에 맞게 데이터(값), 자식을 참조하는 2개의 포인터를 가지고 있다. 이 포인터들은 부모 노드의 자식 노드가 없는 경우를 가정해서 null 이 기본 할당되고, 존재하는 경우에는 해당 자식 노드를 가리키는 참조를 담게 된다.
따라서 이를 반영하면 Node 클래스는 다음 형태가 된다.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
이진 트리 자체의 메소드를 구현하지 않고 각각 node에 값을 넣어서 트리를 만들어 보았다.
const root = new Node(10);
const node1 = new Node(5);
const node2 = new Node(3);
const node3 = new Node(1);
const node4 = new Node(2);
const node5 = new Node(8);
const node6 = new Node(7);
// 10
root.left = node1 // 5
root.right = node2 // 3
// 5
node1.left = node3 // 1
node1.right = node4 // 2
// 3
node2.left = node5 // 8
node2.right = node6 // 7
위와 같이 작성하는 경우 트리 구조를 표현하면 대략 아래 형태가 나온다.
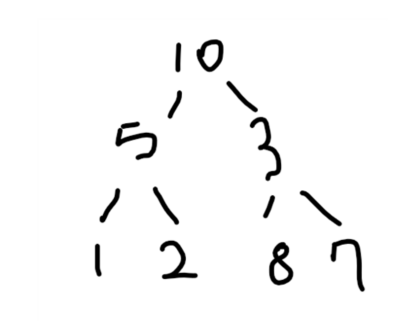
이진트리 순회방식
앞서 살펴본 이진트리는 순회하는 방식이 일반적으로 3 가지 정도가 있다. 중위 순회, 전위 순회, 후위 순회 라고 불리는데, 각각 의미가 무엇인지 정리해보면 다음과 같다.
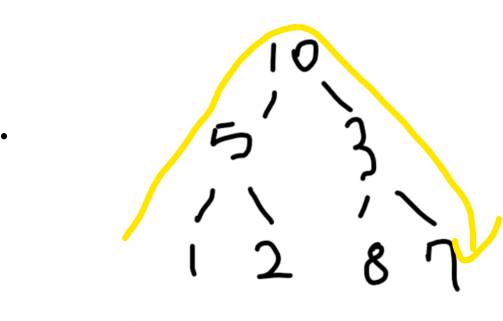
중위 순회(Inorder Traversal) | 왼쪽 하위 > 루트 > 오른쪽 하위
왼쪽 하위트리를 방문한 다음, 루트를 방문 후 마지막으로 오른쪽 하위트리를 방문하는 방식이다.
정리하면, 왼쪽 > 루트 > 오른쪽 이 된다.
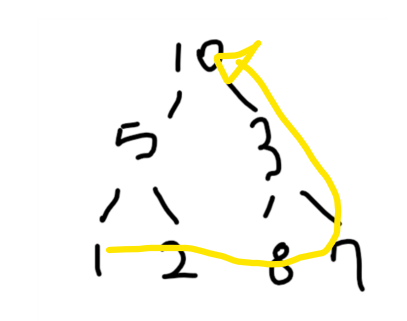
전위 순회(Preorder Traversal) | 루트 > 왼쪽 하위 > 오른쪽 하위
루트에서 시작하여, 왼쪽 하위트리를 순회하고, 오른쪽 하위트리를 순회하는 방식이다.
이 또한 정리해보면 루트 > 왼쪽 > 오른쪽 이 된다.

후위 순회(Postorder traversal) | 왼쪽 하위 > 오른쪽 하위 > 루트
왼쪽 하위 트리를 방문한 다음 오른쪽 하위 트리를 방문하고, 마지막으로 루트를 방문하는 방식이다.
이 경우는 루트가 마지막이므로 왼쪽 > 오른쪽 > 루트 가 된다.
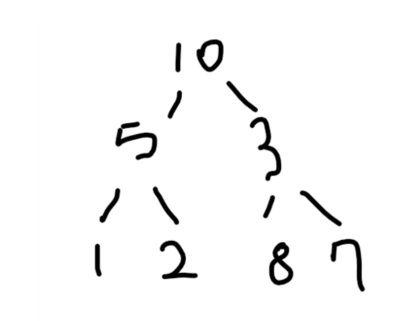
이진 트리 유형
이진트리는 요소가 추가 되는 방식에 따라서 총 5가지 유형으로 구분된다.
Full 이진 트리
모든 자식이 0 혹은 2개로 구성된 이진 트리를 의미한다. 즉, 부모 노드가 가지는 자식 노드는 무조건 0 개 아니면 2개 이어야 만족하는 유형이다.
Perfect 이진 트리
모든 노드가 빠짐없이 빼곡하게 차 있는 형태의 이진 트리이다. 즉, 각각의 부모 노드는 모두 2개의 자식 노드를 가질 때 만족하는 트리 유형이다.
Complete 이진 트리
왼쪽에서 부터 오른쪽 방향으로 자식 노드를 순서대로 채워나갈 때 만족하는 트리 유형이다. 즉, 모든 자식 노드는 무조건 왼쪽에서 부터 채워나가야 하며, 이를 무시하고 띄어 넘는 경우에는 이 유형이 아니다.
참고로 아래 트리의 경우에는 Full, Prefect 트리와 Complete 트리를 모두 만족한다. 만일 여기서 2 라고 적힌 노드가 빠진다면, Full, Complete, Prefect 트리를 모두 만족하지 못하게 된다.
Degenerate 트리
부모 노드가 모두 하나의 자식 노드만 가질 때 만족하는 트리이다. 트리 유형 중 제일 최악이며 피해야 하는 유형이다.
아래 트리에서 10 > 5 > 1 이렇게 일직선으로 하나의 노드만 참조하여 이어지는 형태를 보이며, 이는 연결 리스트하고 별 차이가 없으므로 트리로서의 장점이 사라진다.

Balanced 트리
트리 구조가 균형을 이루도록 유지되는 특별한 형태의 트리이다. 각 노드의 서브 트리 높이가 일정 수준 이상 차이가 나지 않는 경우 이 트리를 만족하게 된다.
대표적인 밸런스드 트리는 AVL 트리와 레드-블랙 트리가 있다.
AVL 트리는 각 노드의 두 자식 서브트리의 높이 차이가 1 이하로 유지되며, 삽입과 삭제 연산 시 에도 이를 유지하기 위해 회전 연산이라는 것을 사용한다고 한다. 이것만 봐도 연산이 복잡해 보인다.
레드-블랙 트리는 특이하게 각 노드를 레드 혹은 블랙 색상으로 표시한다. 자세한 내용은 앞으로 알아가며 정리할 생각이므로 여기서는 이대로만 정리하고 넘어간다.
[나가는 말] 정리
오늘 드디어 이진 트리에 대해 정리해 보았다. 연결 리스트, 스택과 큐, 트리 까지가 쉬운 자료구조라고 하는데, 앞서 살펴본 AVL 트리나 레드-블랙 트리의 경우는 그리 쉬워 보이지 않는다. 또한 연결리스트의 경우에도 헤드와 테일을 같이 고려할 때 연산이 약간 복잡해지는 것을 보면 성능 최적화가 이루어진 자료구조는 그 만큼 복잡해지는 것은 당연해 보인다.
다음 시간에는 이제 이진트리 중에서도 성능이 최적화된 이진 탐색 트리에 대해 간략하게 알아보고 각 연산을 어떻게 구현하는지 정리해보고자 한다.
'알고리즘과 자료구조 > 자료구조' 카테고리의 다른 글
| 자바스크립트로 구현하는 이진 힙 (0) | 2024.06.26 |
|---|---|
| [자료구조] 이진탐색트리와 연산 (0) | 2024.05.01 |
| [자료구조] 배열을 이용한 스택과 큐 구현 (1) | 2024.04.12 |
| 자바스크립트에서 사용되는 주요 배열 메서드의 시간복잡도에 대해서 알아보자? (0) | 2024.04.10 |
| [자료구조] 이중연결리스트 remove 함수(메서드) 만들기 (0) | 2024.04.09 |


