들어가는 말 | 시간복잡도 그래프와 Big 5
이번 시간에는 이진 힙에 대해서 정리해봅니다. 이진 힙은 자료구조 중에서 이진 트리의 한 유형이며 그 중에서도 완전 이진 트리로 불립니다. 완전 이진 트리이므로 보다 삭제, 삽입, 정렬 연산이 쉬운 점이 장점이고, 삽입과 삭제 연산 자체가 log n 시간복잡도를 가지기 때문에, 효율적인 연산이기도 합니다.
예를 들어, 입력 크기가 n일 때, 수행 시간은 log n에 비례하여 증가합니다. 즉, 입력 크기가 두 배가 되면 수행 시간은 log(2n) = log n + log 2로 증가합니다. 이는 두 배가 되는 경우에도 증가폭이 매우 작음을 의미합니다.
아래 시간 복잡도 그래프를 보면 상수 시간복잡도인 O(1) 바로 위에 O(log n) 이 있는 것을 볼 수 있습니다.
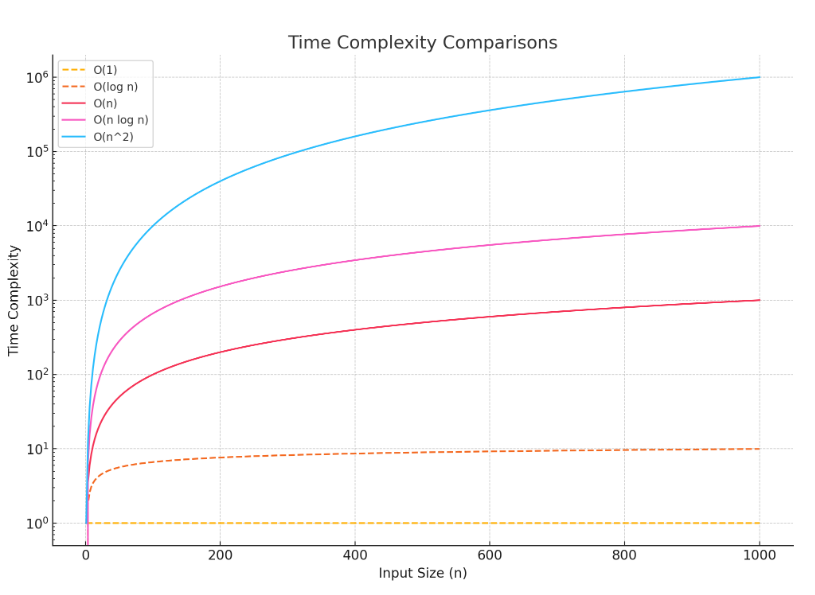
- O(1): 상수 시간 복잡도입니다. 입력 크기 𝑛에 상관없이 일정한 시간이 소요됩니다.
- O(log n): 로그 시간 복잡도입니다. 입력 크기 𝑛 이 증가함에 따라 수행 시간은 천천히 증가합니다.
- O(n): 선형 시간 복잡도입니다. 입력 크기 𝑛 에 비례하여 수행 시간이 증가합니다.
- O(n log n): 선형 로그 시간 복잡도입니다. 입력 크기 𝑛이 증가함에 따라 수행 시간이 𝑛 과 log 𝑛 의 곱에 비례하여 증가합니다.
- O(n^2): 이차 시간 복잡도입니다. 입력 크기 𝑛 이 증가함에 따라 수행 시간은 𝑛2 에 비례하여 매우 빠르게 증가합니다.
이진힙 | 개념
이진힙은 기본적으로 완전 이진 트리입니다. 따라서 일반적인 배열로 변환하기 쉽습니다. 여기서 완전 이진 트리란, 노드를 추가할 때, 좌측에서 우측으로 차례대로 노드를 추가하여 사이사이에 빈 노드가 존재하지 않는 완전한 이진 트리를 말합니다.
힙은 최대 힙 혹은 최소 힙의 상태를 유지해야 합니다. 이 말은 특정 노드를 수정하는 경우, 그 노드가 그 부모노드 보다 크다면 해당 부모노드와 자리를 바꿔주는(스왑) 연산을 수행해야 하고, 이러한 연산을 루트 노드가 있는 위치 혹은 리프 노드 까지 수행해야 하는데, 이를 heapify 라고 부릅니다. 그리고 하향식이냐 상향식이냐에 따라 각각 heapify up 과 heapify down 으로 불립니다.
이진힙은 정말 특이한 점이 하나 있습니다. 최소 힙이든 최대 힙이든 노드를 전부 삭제하고, 삭제된 노드를 새로운 배열로 담아두게 되면, 오름차순 혹은 내림차순으로 정렬이 됩니다. 이러한 정렬을 힙 정렬 이라고 부릅니다.
이진 힙에서 부모노드의 인덱스와 자식 노드의 인덱스
이진 힙에서 부모노드와 자식 노드의 인덱스를 알고 있는 것이 중요합니다. 왜냐 하면, 해당 인덱스를 이용해서 heapify 라는 연산을 수행하기 때문입니다.
아래에 발로 그린 이진 완전 트리가 있습니다.

여기서 2 라는 값을 가지고 있는 노드의 왼쪽 자식 노드의 인덱스를 구한다면 어떻게 해야 할까요? 바로 말씀 드리면, I * 2 + 1 를 계산해주면 됩니다. 이 떄 I 은 2를 담고 있는 노드의 인덱스를 나타냅니다.
예를 들어, 2를 담고 있는 노드의 인덱스는 2 이므로 2 * 2 + 1 = 5 가 나오는데, 여기서 5번째 인덱스에 위치한 노드가 2의 자식 노드가 됩니다. 그럼 오른쪽 자식 노드의 인덱스는 어떻게 구할 수 있을까요? 아시다시피 I * 2 + 2 를 해주면 됩니다.
그럼 자식 노드의 인덱스를 알고 있는 상태에서 부모 노드의 인덱스를 구하려면 어떻게 해야 할까요? 바로 Math.floor((childIndex-1)/2) 를 해주면 됩니다. 이는 왼쪽 자식 노드이든 오른쪽 자식 노드이든 계산하게 되면 부모노드의 인덱스를 가리키게 됩니다.
여기서 요약하고 가겠습니다.
// index : 부모 노드의 인덱스
// 2 의 왼쪽 자식 노드
const leftChildNodeIndex = index*2+1
// 2의 오른쪽 자식 노드
const rightChildNodeIndex = index*2+2
// 왼쪽 자식 노드의 부모 노드 인덱스
const parentIndex = Math.floor((leftChildNodeIndex-1)/2)
// 오른쪽 자식 노드의 부모 노드 인덱스
const parentIndex = Math.floor((rightChildNodeIndex-1)/2)
중요하므로 꼭 알아둡시다.
최대 힙과 최소 힙
앞서 이진 힙은 최대 힙과 최소 힙이 있다고 언급하였습니다. 그리고 해당 힙의 성질을 유지해야 한다고 말씀드렸습니다. 그럼 최대 힙과 최소 힙은 어떻게 유지가 되어야 하는 것일까요? 여기서는 이에 대해서 정리해보고 갑니다.
최대힙
최대힙은 루트 노드의 값 > 그 자식 노드의 값 > 그 자식의 자식 노드의 값이 되어야 합니다. 이렇게 글로만 보면 이해가 되지 않겠죠? 그래서 발로 그린 그림을 다시 가져왔습니다. 아래 트리를 보시면 자식 노드를 가진 부모 노드는 모두 그 자식 노드의 값보다 큰 값을 가지고 있습니다. 만일 삽입 연산, 삭제 연산을 수행하더라도 이 규칙은 준수되어야 하므로 앞서 말한 heapify 라는 연산이 수행되는 것입니다.
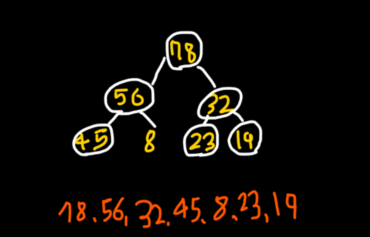
| 참고로 삽입 연산의 경우에는 트리의 마지막 순서에 노드를 추가하고, 해당 노드로 부터 루트 노드 까지 스왑 하는 과정을 수행하기 때문에 상향식으로 heapify 가 수행됩니다. 이를 heapify up 연산이라고 부릅니다. 반면, 삭제 연산의 경우에는 우선적으로 루트 노드를 제거하고, 루트 노드의 자리에는 트리의 마지막 지점에 있는 노드를 할당하게 됩니다. 이 때 루트 노드에 온 노드와 하위에 있는 노드 간에 값을 비교해서 최대힙의 경우 최댓값을 가진 노드와 바꿔주는 연산을 하향식으로 heapify 연산을 수행합니다. 이를 heapify down 연산이라고 부릅니다. |
최소힙
최대 힙의 반대는 최소 힙입니다. 당연히 최소 힙은 루트 노드의 값이 가장 작은 값이 들어와야 합니다. 앞서 최대힙에서 보여드린 트리 이미지에서 78 이라는 값을 가진 노드의 자리에 8이라는 값을 가진 노드가 들어온다고 보면 됩니다. 만일 최대힙인 노드를 최소힙으로 변경하고자 한다면, 모든 노드를 비교하고 스왑하여 바꿔주는 작업이 필요할 것임을 짐작할 수 있습니다.
시간복잡도와 공간복잡도
이론의 마지막 차례로 시간복잡도와 공간복잡도에 대해서 알아보고 가겠습니다. 직접 작성하기는 귀찮아서 지피티에게 만들어 달라고 하였습니다. 여기서 찾기 연산의 경우 상수 시간복잡도라고 나와 있는데, 이는 찾고자 하는 값이 최솟값 혹은 최댓값으로 한정되어 있어서 그런 것으로 보입니다. 하지만, 찾고자 하는 노드가 트리의 중간이나 끝에 있다면 순차적으로 탐색해야 하므로 선형 시간 복잡도도 가능해 보입니다.
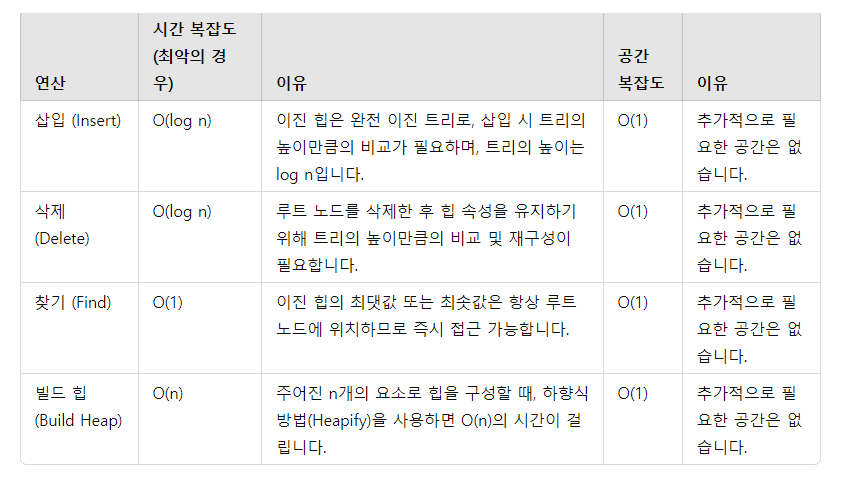
나중에 빌드 힙이라고 나와 있는 heapify 연산을 수행해보면, O(1/2n) 의 시간 복잡도를 수행하는 것을 볼 수 있습니다. 빅오 계산 시에는 앞의 차수를 제외하기 때문에 O(n) 이 됩니다.
또한 삭제와 삽입 시 O(log n) 이 걸리는 이유도 이진 힙의 높이가 log n 이 되기 때문입니다.
구현
구현에 사용되는 코드는 최대 힙이 기준입니다. 사실 최대 힙과 최소 힙을 구분하는 코드는 조건 문에서 > 이거냐, < 요거냐의 차이 밖에 없습니다.
이전에는 각 코드를 나눠서 설명하는 방식이었는데, 굳이 그럴 필요가 없는 것 같아서 하나의 스니펫에 모두 정리합니다.
최대 힙
힙을 구현하는 방법은 다양합니다. 하지만 구조 자체는 크게 다를게 없습니다. 아래 힙의 경우에는 재귀를 최대한 활용하고 있습니다. 아래에서 leftIndex < this.arr.length 이렇게 비교하는 if 가 보일겁니다. 해당 조건문은 자식요소가 힙의 범위 내에 존재하고 있는지를 확인합니다. 인덱스는 배열의 길이 보다 무조건 작아야 하는데, 반대로 크다면 힙의 범위를 벗어난 것이므로 조건문을 실행하지 않습니다
class MaxHeap {
arr = []
// 부모 인덱스
#parentIndex(index) {
return Math.floor((index - 1) / 2)
}
// 왼쪽 자식 인덱스
#leftChildIndex(index) {
return 2 * index + 1
}
// 오른쪽 자식 인덱스
#rightChildIndex(index) {
return 2 * index + 2
}
#heapifyUp(index) {
if (index === 0) return
if (this.arr[this.#parentIndex(index)] < this.arr[index]) {
const temp = this.arr[index]
this.arr[index] = this.arr[this.#parentIndex(index)]
this.arr[this.#parentIndex(index)] = temp
this.#heapifyUp(this.#parentIndex(index))
}
}
insert(value) {
const index = this.arr.length // 인덱스
this.arr[index] = value // 해당 인덱스 자리에 노드 추가
this.#heapifyUp(index) // 상향식 스왑(부모와 자식 비교)
}
#heapifyDown(index) {
const leftIndex = this.#leftChildIndex(index)
const rightIndex = this.#rightChildIndex(index)
let largest = index
if (leftIndex < this.arr.length && this.arr[leftIndex] > this.arr[largest]) {
largest = leftIndex
}
if (rightIndex < this.arr.length && this.arr[rightIndex] > this.arr[largest]) {
largest = rightIndex
}
if (largest !== index) {
const temp = this.arr[index]
this.arr[index] = this.arr[largest]
this.arr[largest] = temp
this.#heapifyDown(largest)
}
}
removeRoot() {
if (this.arr.length === 0) return
const root = this.arr[0] // 루트 요소 제거
if (this.arr.length === 1) {
this.arr.pop()
return root
}
this.arr[0] = this.arr.pop() // 마지막 요소 꺼내서 루트 자리로
// 최대 힙이 무너진 경우 맞추기 위해 루트 인덱스 -> 리프 인덱스 방향으로
this.#heapifyDown(0)
return root
}
// 힙 정렬
sort() {
const sortedArr = []
while (this.arr.length > 0) {
sortedArr.push(this.removeRoot())
}
return sortedArr
}
// 특정 노드 수정
update(value, newValue) {
for (let i = 0; i < this.arr.length; i++) {
if (this.arr[i] === value) {
this.arr[i] = newValue
break
}
}
let parentIndex = Math.floor((this.arr.length / 2 - 1))
for (let i = parentIndex; i >= 0; i--) {
this.#heapifyDown(i)
}
}
}
const maxHeap = new MaxHeap()
maxHeap.insert(5)
maxHeap.insert(30)
maxHeap.insert(35)
maxHeap.insert(15)
maxHeap.insert(7)
console.log(maxHeap.sort())
console.log(maxHeap.arr)
최소힙
최소 힙의 경우 앞서 언급했듯이 부호을 반대로 바꿔주고, 일부 조건을 조금만 수정하기만 하면됩니다.
class MinHeap {
arr = []
// 부모 인덱스
#parentIndex(index) {
return Math.floor((index - 1) / 2)
}
// 왼쪽 자식 인덱스
#leftChildIndex(index) {
return 2 * index + 1
}
// 오른쪽 자식 인덱스
#rightChildIndex(index) {
return 2 * index + 2
}
#heapifyUp(index) {
if (index === 0) return
if (this.arr[this.#parentIndex(index)] > this.arr[index]) {
const temp = this.arr[index]
this.arr[index] = this.arr[this.#parentIndex(index)]
this.arr[this.#parentIndex(index)] = temp
this.#heapifyUp(this.#parentIndex(index))
}
}
insert(value) {
const index = this.arr.length // 인덱스
this.arr[index] = value // 해당 인덱스 자리에 노드 추가
this.#heapifyUp(index) // 상향식 스왑(부모와 자식 비교)
}
#heapifyDown(index) {
const leftIndex = this.#leftChildIndex(index)
const rightIndex = this.#rightChildIndex(index)
let smallest = index
// 왼쪽 자식 인덱스가 배열 길이 보다 작다는 것은 힙의 범위를 벗어났다는 의미
if (leftIndex < this.arr.length && this.arr[leftIndex] < this.arr[smallest]) {
smallest = leftIndex
}
if (rightIndex < this.arr.length && this.arr[rightIndex] < this.arr[smallest]) {
smallest = rightIndex
}
if (smallest !== index) {
const temp = this.arr[index]
this.arr[index] = this.arr[smallest]
this.arr[smallest] = temp
this.#heapifyDown(smallest)
}
}
removeRoot() {
if (this.arr.length === 0) return
const root = this.arr[0] // 루트 요소 제거
if (this.arr.length === 1) {
this.arr.pop()
return root
}
this.arr[0] = this.arr.pop() // 마지막 요소 꺼내서 루트 자리로
// 최대 힙이 무너진 경우 맞추기 위해 루트 인덱스 -> 리프 인덱스 방향으로
this.#heapifyDown(0)
return root
}
// 힙 정렬
sort() {
const sortedArr = []
while (this.arr.length > 0) {
sortedArr.push(this.removeRoot())
}
return sortedArr
}
// 특정 노드 수정
update(value, newValue) {
for (let i = 0; i < this.arr.length; i++) {
if (this.arr[i] === value) {
this.arr[i] = newValue
break
}
}
let parentIndex = Math.floor((this.arr.length / 2 - 1))
for (let i = parentIndex; i >= 0; i--) {
this.#heapifyDown(i)
}
}
}
const minHeap = new MinHeap()
minHeap.insert(5)
minHeap.insert(30)
minHeap.insert(35)
minHeap.insert(15)
minHeap.insert(7)
console.log(minHeap.sort())
console.log(minHeap.arr)
이렇게 구현된 이진 힙은 어디에 쓰이는지??
이렇게 구현할 수 있는 이진 힙은 어디에 사용될까요? 대표적으로는 힙 정렬 알고리즘과 우선순위 큐 를 구현할 때 쓰이고 있습니다. 이를 포함해서 어디에 활용이 될 수 있는지 정리해봅시다.
우선순위 큐(Priority Queue) | 각 요소에 우선순위가 부여된 데이터 구조로, 높은 우선순위의 요소가 먼저 처리
우선순위 큐는 각 요소에 우선순위가 부여된 데이터 구조로, 높은 우선순위의 요소가 먼저 처리됩니다. 이진 힙은 우선순위 큐를 효율적으로 구현하는 데 사용됩니다.
최소 힙(Min Heap): 최상위 요소가 최소값이 되는 힙으로, 낮은 우선순위부터 처리됩니다.
최대 힙(Max Heap): 최상위 요소가 최대값이 되는 힙으로, 높은 우선순위부터 처리됩니다.
힙 정렬(Heap Sort)
사실 힙 정렬은 앞서 기능 구현 시 같이 구현이 되었습니다. 이진 힙은 특이하게도, 제거한 요소를 순서대로 나열하면 오른차순 혹은 내림차순으로 정렬이 됩니다.
배열을 힙 구조로 변환합니다.
힙에서 최상위 요소를 제거하여 정렬된 배열에 추가합니다.
힙의 크기를 줄이고 힙 속성을 유지하도록 재정렬합니다.
이를 반복하여 모든 요소를 정렬합니다.
힙 정렬은 최악의 경우에도 O(n log n)의 시간 복잡도를 가진다고 합니다. 따라서 안정 정렬은 아니지만 공간 복잡도 측면에서 효율적입니다. 공간을 늘리기 보다 삭제된 공간 만큼만 공간을 복원하므로 당연해 보입니다.
그래프 알고리즘
이진 힙은 그래프 탐색 알고리즘에서 중요한 역할을 합니다.
- 다익스트라(Dijkstra)의 최단 경로 알고리즘: 우선순위 큐로 사용되어 최단 경로를 찾는 데 효율적입니다.
- 프림(Prim)의 최소 신장 트리 알고리즘: 최소 신장 트리를 찾는 데 사용되며, 가중치가 가장 작은 간선을 우선적으로 선택합니다.
그 외에도 시뮬레이션 시스템, 온라인 알고리즘 등에 쓰인다고 합니다. 현재 로서는 처음 들어보는 알고리즘이 많이 보이네요. 이런 예시의 알고리즘도 한 번 찾아보면 좋은 공부가 될 것 같습니다.
참고자료
http://www.ktword.co.kr/test/view/view.php?no=6106
https://en.wikipedia.org/wiki/Heap_(data_structure)
'알고리즘과 자료구조 > 자료구조' 카테고리의 다른 글
| [자료구조] 이진탐색트리와 연산 (0) | 2024.05.01 |
|---|---|
| [자료구조] 이진(+탐색)트리 전 개요 (0) | 2024.04.24 |
| [자료구조] 배열을 이용한 스택과 큐 구현 (1) | 2024.04.12 |
| 자바스크립트에서 사용되는 주요 배열 메서드의 시간복잡도에 대해서 알아보자? (0) | 2024.04.10 |
| [자료구조] 이중연결리스트 remove 함수(메서드) 만들기 (0) | 2024.04.09 |


