이진탐색트리
이진탐색트리는 각 노드에 최대 두 개의 자식을 가지는 것은 이진트리와 같으나, 한 가지 눈에 띄는 차이점이 존재한다. 바로, 부모 노드의 왼쪽 자식 노드는 부모 노드보다 작은 값을 가져야 하고, 오른쪽 자식 노드는 반대로 큰 값을 가져야 한다.
즉, 다음과 같은 형태가 되어야 한다.
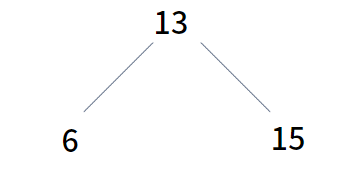
이 규칙은 자식 노드를 가지는 모든 부모 노드가 공통적으로 가지는 규칙 이므로 꼭 지켜주어야 한다.
이진탐색 트리 구현 | Node Class
이진탐색트리는 연결리스트하고 비교 했을 때 Node 클래스를 가지는 것은 동일하다. 다만, 트리의 Node 클래스는 head 라고 하는 참조 필드가 아닌, 왼쪽 자식 노드를 참조하는 left 와 오른쪽 자식 노드를 참조하는 right 가 있다.
즉, 다음과 같은 형식으로 Node class 를 구현한다.
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
이진탐색트리 구현 | BinarySearchTree Class
이진탐색트리 클래스는 초기의 형태의 경우 root 라는 프로퍼티 하나만 존재한다. 따라서 초기 틀만 만들어보면 다음과 같다.
class BinarySearchTree {
constructor(){
this.root = null;
}
}
이진탐색트리 구현 | insert()
이진탐색트리에서 삽입 연산을 할 때는 루트 노드 부터 시작해서 아랫 방향으로 나아가는 방식으로 연산이 이루어진다. 여기서 중요한 포인트는 삽입하고자 하는 data 가 트리에 중복되어 존재하면 안 된다는 점, 부모노드의 값보다 작은 값은 왼쪽 자식 노드의 트리로, 큰 값은 오른쪽 자식 노드 트리의 뿌리를 타고 내려가야 한다는 점이다.
이를 염두에 두고, insert 함수를 구현하면 다음과 같다. 참고로 아랫 방향으로 탐색을 이어갈 때 재귀를 이용할 수도 있지만 현재 구현하고자 하는 방식처럼 반복문을 사용할 수 있다. 성능상 약간의 이점을 생각한다면 재귀가 더 나을 수도 있을 것 같긴하다. 방법은 다양하므로 상황에 맞게 쓰면된다고 생각한다.
inset(data) {
const newNode = new Node(data);
// 루트 노드가 비어 있으면 새로 추가한 노드를 루트 노드로 설정
if(this.root === null) return this.root = newNode;
// 현재 상태를 insert 함수가 실행되는 동안 로컬에서 유지하기 위해 currentNode 에 루트 노드를 담는다.
let currentNode = this.root;
// 트리의 끝 까지 탐색하기 위해 무한루프 설정(내부에서 return 을 통해 바로 탈출 가능)
while(true) {
// 중복된 데이터는 필요없기 때문에 바로 탈출한다.
if(currentNode.data === data) return // 혹은 return undefined
// 왼쪽 노드 : 부모 노드의 값이 자식 노드 값보다 큰 경우 진행
if(currentNode.data > data) {
// 왼쪽 자식노드가 비어있으면 해당 자리에 새노드를 할당하고,
// 기존 노드가 있다면 다음 탐색을 위해 currentNode 변수에 담는다.
if(currentNode.left === null) return currentNode.left = newNode
return currentNode = currentNode.left
}
// 오른쪽 노드 : 부모 노드의 값이 자식 노드 보다 작은 경우 진행
if(currentNode.data < data) {
// 오른쪽 자식노드가 비어있으면 해당 자리에 새노드를 할당하고,
// 기존 노드가 있다면 다음 탐색을 위해 currentNode 변수에 담는다.
if(currentNode.right === null) return currentNode.right = newNode
return currnetNode = currentNode.right
}
}
}
설명은 주석으로 모두 달아두었는데, 핵심은 두 가지로 정리된다. 하나는 중복된 값은 허용하지 않는다는 것, 두 번째는 부모 노드의 값이 자식노드의 값보다 크면 왼쪽 노드를 다음 참조로, 작다면 오른쪽 노드로 다음 참조를 이동하며 탐색을 이어나가는 것이다.
2024.06.10 재귀 로직 추가
이전에 insert 메서드를 구현했을 때는 while 문을 사용하여 무한 루프를 도는 방식으로 처리를 했었는데, 재귀를 통해 탐색하는 방식으로 작성해보았다. 확실히 while 로 처리했을 때 보다 로직이 단순화 되고 이해하기 쉬워진 것 같다.
class Node {
constructor(value){
this.value = value;
this.left = null;
this.right= null;
}
}
class Bst {
root = null;
#insert(node, value){
if(node.value > value) {
if(!node.left) node.left = new Node(value)
else this.#insert(node.left, value)
} else {
if(!node.right) node.right = new Node(value)
else this.#insert(node.right, value)
}
}
insert(value){
if(!this.root) this.root = new Node(value)
else this.#insert(this.root, value)
}
}
const bst = new Bst();
bst.insert(10)
bst.insert(5)
bst.insert(11)
bst.insert(12)
console.log(bst)
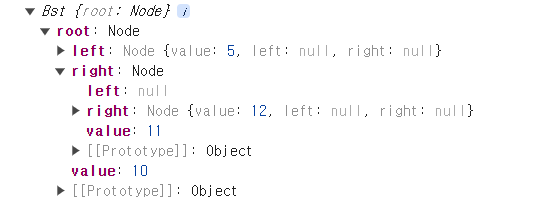
이진탐색트리 구현 | search()
이번에 구현할 메소드는 이진탐색트리에서 특정한 값을 가진 노드를 찾는 연산을 수행하는 find 메소드이다. insert 메소드와의 차이점은 크게 없고, 있다면 해당하는 data 를 찾는 순간 해당 데이터를 담고 있는 노드를 반환하는 점인 것 같다.
일단 구현 전에 중요한 키 포인트를 언급해보면 다음과 같다.
첫 째, root 노드가 비어 있다면 연산을 수행하지 않고 바로 return 한다.
둘 째, 루트 노드를 지나 현재 노드가 null이 되는 지점(비어 있는 경우)은 리프 노드의 끝에 도달한 것이므로 return 한다.
셋 째, 찾고자 하는 data 가 부모노드의 값보다 작다면 왼쪽 방향으로, 크다면 오른쪽 방향으로 순회한다.
search(data) {
if(this.root === null) return
let currentNode = this.root;
let isMatch = false;
// data 를 찾거나 트리의 끝에 도달하면 탈출
while(isMatch !== true && currentNode) {
// 부모노드의 값이 더 크다면 왼쪽 하위 트리로
if(currentNode.data > data) currentNode = currentNode.left
// data 가 더 크다면 오른쪽 하위 트리로
else if(currentNode.data < data) currentNode = currentNode.right
// 크지도 작지도 않으면 같다는 의미이므로 isMatch 를 true 로 변경
else isMatch = true;
}
// 순회동안 찾지 못하는 경우에는 바로 탈출
if(!isMatch) return;
// 순회 동안 찾은 경우에는 data 를 넣은 노드를 반환
return current;
}
로직 자체가 단순하기 때문에, 별도로 설명할 것은 없어 보인다. 핵심은 일치하는 값을 찾을 때 까지 재귀적으로 참조되는 노드를 바꿔가는 것이 다 이므로 이 부분만 염두에 두고 구현하면 될 것 같다.
앞서 구현한 search 메소드 내에서 isMatch 라는 값의 일치유무를 판별하는 변수를 선언하여 사용하였는데, 굳이 저렇게 하지 않고 while 문 내부에서 값이 일치하면 바로 탈출하게 로직을 작성해도 동일한 동작을 수행할 듯하다. 이 부분은 입맛에 맞게 응용하면 될 부분이다.
이진탐색 트리 search 재귀 호출 구현 추가(2024.06.11)
앞서 작성한 이진탐색 search 함수는 하나의 메소드 내부에서 while 문을 사용하여 조건을 만족하는 값을 찾을 때 까지 트리 전체를 순회하도록 하고 있다. 하지만, 이로 인해 코드의 가독성이 떨어지는 문제가 있었다. 하지만 재귀 호출을 이용하는 경우에는 이러한 로직을 더욱 더 가시적으로 효율적으로 처리할 수 있게 해준다.
#search(node, value){
if(!node) return undefined // 트리의 끝에 도달한 경우 탈출
if(node.value === value) return node // 타겟 노드를 찾은 경우
if(node.value>value){ // 타켓노드가 작다면 왼쪽 뿌리로
return this.#search(node.left, value)
} else { // 타겟노드가 크다면 오른쪽 뿌리로
return this.#search(node.right, value)
}
}
search(value){
if(!this.root) return undefined // 루트 노드가 없으면 탈출
else return this.#search(this.root, value) // 최종결과 반환
}
[참고] GPT 답변 - 이진탐색트리 재귀를 적용한 구현
아래는 이진탐색트리를 재귀를 사용하여 구현하고, 완성된 이진탐색트리를 순회하는 몇 가지 방식에 대한 구현을 포함한 예시이다(타 예시).
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor() {
this.root = null;
}
/** 삽입 연산 */
insert(data) {
const newNode = new Node(data);
if (this.root === null) { // 루트 노드가 없으면 추가
this.root = newNode;
} else { // 기존 노드가 있으면, 삽입 연산 재귀 호출
this.insertNode(this.root, newNode);
}
}
insertNode(node, newNode) {
// 왼쪽 자식 노드
if (newNode.data < node.data) {
if (node.left === null) { // 기존 노드의 왼쪽 자식 노드가 없으면 새노드 추가
node.left = newNode;
} else { // 왼쪽 자식 있으면 삽입 연산 재귀 호출
this.insertNode(node.left, newNode);
}
// 오른쪽 자식 노드
} else {
if (node.right === null) { // 기존 노드 오른쪽 자식 노드 없으면 새노드 추가
node.right = newNode;
} else { // 오른쪽 자식 있으면 삽입연산 재귀 호출
this.insertNode(node.right, newNode);
}
}
}
/** 검색 연산 */
search(data) {
return this.searchNode(this.root, data);
}
searchNode(node, data) {
if (node === null) { // 루트 노드 비었으면 이른 반환(트리 자체가 비어있는 경우)
return false;
}
// 찾으려는 노드의 값이 기존 노드의 값보다 작으면 왼쪽
if (data < node.data) {
return this.searchNode(node.left, data);
// 찾으려는 노드의 값이 기존 노드의 값보다 크면 오른쪽
} else if (data > node.data) {
return this.searchNode(node.right, data);
// 크지도 작지도 않은 상태 즉, 동일한 노드의 값을 가지면 찾았으므로 탈출
} else {
return true;
}
}
/** 삭제 연산 */
remove(data) {
this.root = this.removeNode(this.root, data);
}
removeNode(node, key) {
if (node === null) { // 트리 자체가 비었으면 제거할게 없으므로 탈출
return null;
}
if (key < node.data) {
node.left = this.removeNode(node.left, key);
return node;
} else if (key > node.data) {
node.right = this.removeNode(node.right, key);
return node;
} else {
if (node.left === null && node.right === null) {
node = null;
return node;
}
if (node.left === null) {
node = node.right;
return node;
} else if (node.right === null) {
node = node.left;
return node;
}
const aux = this.findMinNode(node.right);
node.data = aux.data;
node.right = this.removeNode(node.right, aux.data);
return node;
}
}
findMinNode(node) {
while (node.left !== null) {
node = node.left;
}
return node;
}
inorder(node) {
if (node !== null) {
this.inorder(node.left);
console.log(node.data);
this.inorder(node.right);
}
}
preorder(node) {
if (node !== null) {
console.log(node.data);
this.preorder(node.left);
this.preorder(node.right);
}
}
postorder(node) {
if (node !== null) {
this.postorder(node.left);
this.postorder(node.right);
console.log(node.data);
}
}
}
// Example usage:
const bst = new BinarySearchTree();
bst.insert(15);
bst.insert(10);
bst.insert(20);
bst.insert(8);
bst.insert(12);
bst.insert(17);
bst.insert(25);
console.log("Inorder traversal:");
bst.inorder(bst.root); // Output: 8 10 12 15 17 20 25
bst.remove(12);
console.log("Inorder traversal after removing 12:");
bst.inorder(bst.root); // Output: 8 10 15 17 20 25
이진탐색트리에서의 시간복잡도와 공간복잡도
시간복잡도
탐색, 삽입, 삭제 연산
| 최선의 경우 (Balanced Tree): O(log n) |
| 트리가 균형 잡혀 있는 경우, 트리의 높이는 O(log n)이 됩니다. 각 연산은 높이만큼만 진행되므로 시간복잡도는 O(log n)입니다. |
| 최악의 경우 (Unbalanced Tree): O(n) |
| 트리가 한쪽으로 치우친 경우(예: 한쪽으로만 연속해서 삽입), 트리의 높이는 O(n)이 됩니다. 이 경우 각 연산은 전체 노드를 순회해야 하므로 시간복잡도는 O(n)입니다. |
공간복잡도
노드 저장 공간
| 모든 경우: O(n) |
| 트리의 각 노드는 하나의 포인터를 사용하여 왼쪽 및 오른쪽 자식을 가리킵니다. 노드의 개수가 n개일 때, 공간복잡도는 O(n)입니다. 즉, 노드의 개수가 증가할 때 마다 메모리 공간을 차지 하는 참조 공간의 수도 선형적으로 증가합니다. |
재귀 호출 공간
| 균형 트리: O(log n) |
| 재귀 호출은 트리의 높이만큼 스택 프레임을 사용합니다. 균형 트리에서는 높이가 O(log n)입니다. |
| 비균형 트리: O(n) |
| 트리가 한쪽으로 치우친 경우, 높이는 O(n)이고 재귀 호출 스택도 그만큼 쌓이게 됩니다. |
이진탐색 트리(BST)에서 높이가 log n이 되는 과정은 트리가 균형 잡힌 경우입니다. 이를 이해하기 위해서는 이진탐색 트리의 구조와 성질을 이해해야 합니다.
이진탐색 트리의 구조와 성질
각 노드는 최대 두 개의 자식 노드를 가질 수 있습니다. 왼쪽 자식 노드는 부모 노드보다 작은 값을 가지며, 오른쪽 자식 노드는 부모 노드보다 큰 값을 가집니다.
균형 잡힌 트리
균형 잡힌 트리는 노드가 균등하게 분포되어 트리의 높이가 최소화된 상태를 말합니다. 이상적인 경우, 각 레벨(level)에는 가능한 한 많은 노드가 존재하게 됩니다.
트리의 높이가 log n이 되는 이유
트리의 레벨당 노드 수
(루트 레벨) 트리의 루트(root)는 1개의 노드를 가집니다.
(1레벨) 루트의 자식 노드(레벨 1)는 2개의 노드를 가질 수 있습니다.
(2레벨) 레벨 2는 최대 4개의 노드를 가질 수 있습니다.
(3레벨) 레벨 3는 최대 8개의 노드를 가질 수 있습니다.
즉, 1레벨이 증가할 때 마다 2^n 제곱 씩 노드를 가질 수 있으므로, 레벨 ℎ 에서는 최대 2^h 만큼의 노드를 가질 수 있습니다.
노드의 총 개수
트리의 높이를 h라고 할 때, 트리의 총 노드 수 n 다음과 같이 표현할 수 있습니다.
| n=1+2+4+8+…+2^h |
이는 등비 수열의 합으로, 𝑛 ≈ 2^(ℎ +1)−1 로 근사할 수 있습니다. 여기서 상수항은 무시해도 되므로 𝑛≈2^ℎ 로 단순화할 수 있습니다.
높이 계산
𝑛 ≈ 2^ℎ의 양변에 로그를 취하면, 다음과 같은 식을 얻습니다. log2n≈h
즉, 트리의 높이 ℎ는 log 𝑛 에 비례하게 됩니다. 따라서, 이진탐색 트리가 균형 잡힌 경우 트리의 높이는 log n 이 됩니다.
이 높이는 이진탐색, 삽입, 삭제 연산의 시간복잡도를 결정짓는 주요 요소입니다. 균형 잡힌 트리에서는 이러한 연산들이 O(log n)의 시간복잡도로 수행될 수 있습니다.
예시를 통한 설명
다음의 간단한 예시를 통해 설명하겠습니다.
예시 1: 균형 잡힌 트리
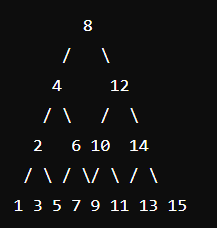
이 트리는 15개의 노드를 가지고 있으며, 높이는 3입니다. 이는 log 15 ≈ 3.9 일 때 즉, 2^3.9 가 될 때 15에 근사( ≈ ) 하므로 log n 에 근접합니다.
즉, 트리의 높이 만큼 연산을 수행한다고 단순화할 수 있으므로 시간복잡도는 O(log n)이 됩니다.
예시 2: 비균형 트리

이 트리는 5개의 노드를 가지고 있지만, 높이는 4입니다. 이 경우 높이는 log 5 ≈ 2.3 이 되는데, 즉, 2^2.3 이 될 때 5에 근사하게 됩니다. 이는 5개의 노드를 트리에 추가하는 연산 횟수가 트리의 높이 만큼 진행되지 않는다는 사실을 증명하는 것입니다.
즉, 현재 연산의 횟수는 n 만큼 선형적으로 증가하기 때문에 시간복잡도는 O(n) 으로 단순화할 수 있습니다.
'알고리즘과 자료구조 > 자료구조' 카테고리의 다른 글
| 자바스크립트로 구현하는 이진 힙 (0) | 2024.06.26 |
|---|---|
| [자료구조] 이진(+탐색)트리 전 개요 (0) | 2024.04.24 |
| [자료구조] 배열을 이용한 스택과 큐 구현 (1) | 2024.04.12 |
| 자바스크립트에서 사용되는 주요 배열 메서드의 시간복잡도에 대해서 알아보자? (0) | 2024.04.10 |
| [자료구조] 이중연결리스트 remove 함수(메서드) 만들기 (0) | 2024.04.09 |


